At first, I thought it would be easier or at least less destructive just to use a keyboard connector on a piece of breakout board with a power switch attached to it.
The connector used on ThinkPad R61 (and on plenty of other models of similar age) is JAE AA01B-P040VA1. However, as it turns out, it’s nearly impossible to procure this thing. They seem to be available only in bulk through some Chinese distributors.
Seems like the only thing left is to solder the button straight to the motherboard. This can be done by soldering a push button to 10th top-left pin and to any of ground pads at the keyboard connector:

However, since R61 comes with an unpopulated docking station connector which also exposes the power button pad, it’s actually easier to use it instead. The pads are covered with solder mask, so it should be removed with sandpaper before soldering. Here we would need to connect 2nd bottom-right pad with any of the ground pads:



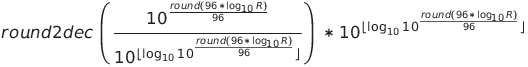 Where R is the resistance, round() is round to nearest integer function, and round2decimal() is round to 2 decimal places function.
Where R is the resistance, round() is round to nearest integer function, and round2decimal() is round to 2 decimal places function.